Marine Predators Algorithm
Marine Predators Algorithm (MPA) is a nature-inspired optimization method that follows the rules that naturally govern in optimal foraging strategy and encounters rate policy between predator and prey in marine ecosystems.
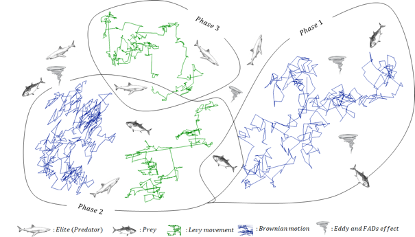
Lévy strategy is a widespread pattern among marine predators (e.g. sharks, tunas, marlines) when searching for food in a prey-sparse environment, but when it comes to foraging in a prey-abundant area, the pattern is prevalently switched to Brownian motion [1]. The optimal encounter rate policy in biological interaction between predator and prey is also dependent on the type of the movement that each of the predator/prey is taking and the velocity ratio of prey to predator [2].
The following highlights summarize the governing policies for the optimal foraging and interactions and memories in marine predators:
- Marine predators use Lévy strategy for the environment with a low concentration of prey while employing Brownian movement for the areas with abundant prey;
- They show the same percentages of Lévy and Brownian movement during their lifetime of traversing different habitats;
- Due to the environmental effects such as natural (eddy formation) or human-caused (FADs), they change their behavior to hopefully find areas with a different distribution of prey;
- In low-velocity ratio (v=0.1), the best strategy for a predator is Lévy; either prey is moving in Brownian or Lévy;
- In the unit velocity ratio (v=1), if prey moves in Lévy, the best strategy for a predator is Brownian. Other scenarios are dependent on system size;
- In high-velocity ratio (v?10) the best strategy for a predator is not moving at all. In this case, either prey is moving Brownian or Lévy; and
- They take advantage of good memory in reminding of their associates as well as the location of successful foraging.
Based on these highlights, the MPA optimization process is divided into three main phases, considering different velocity ratioes and at the same time mimicking the entire life of a predator and prey: (1) in high velocity ratio, or when prey is moving faster than predator, (2) in unit velocity ratio, or when both predator and prey are moving at almost same pace, and (3) in low velocity ratio, when predator is moving faster than prey.
Besides the three phases defined for optimization, some natural and human-caused environmental issues such as eddy formation and FAD’s effect are mathematically modeled to include in the MPA.
In this work, MPA was developed and its performance was evaluated against twenty-nine test functions, test suite of CEC-BC-2017, randomly generated landscape, three engineering benchmarks, and two real-world engineering design problems in the areas of ventilation and building energy performance. MPA was compared with three classes of existing optimization methods, including 1) GA and PSO as the most well-studied metaheuristics, 2) GSA, CS and SSA as almost recently developed algorithms and 3) CMA-ES, SHADE and LSHADE-cnEpSin as high performance optimizers and winners of IEEE CEC competition. Among all methods, MPA gained the second rank and demonstrated very competitive results compared to LSHADE-cnEpSin as the best performing method and one of the winners of CEC 2017 competition. The statistical post hoc analysis revealed that MPA can be nominated as a high-performance optimizer and is a significantly superior algorithm than GA, PSO, GSA, CS, SSA and CMA-ES while its performance is statistically similar to SHADE and LSHADE-cnEpSin.
You can download the main paper here. You can download the MATLAB source code here.
If you don’t have access to the paper, just leave me a message at afaramar@hawk.iit.edu or afshin.faramarzi@gmail.com and I will get back to you soon.
Project lead: Afshin Faramarzi
Co-authors: Mohammad Heidarinejad, Seyedali Mirjalili, and Amir Gandomi
References:
[1] Humphries, N. E., Queiroz, N., Dyer, J. R. M., Pade, N. G., Musyl, M. K., Schaefer, K. M., Fuller, D. W., Brunnschweiler, J. M., Doyle, T. K., Houghton, J. D. R., Hays, G. C., Jones, C. S., Noble, L. R., Wearmouth, V. J., Southall, E. J., & Sims, D. W. (2010). Environmental context explains Lévy and Brownian movement patterns of marine predators. Nature, 465(7301), 1066.
[2] Bartumeus, F., Catalan, J., Fulco, U. L., Lyra, M. L., & Viswanathan, G. M. (2002). Optimizing the encounter rate in biological interactions: Lévy versus Brownian strategies. Physical Review Letters, 88(9), 097901.